Let’s code it: Compact symmetric matrices
You need to store a symmetric matrix, but you don’t want to waste space… The following should help you!
We can declare a data structure that contains all the unique data to avoid the duplication and we can do some tricks with the indices to still get the correct data.
First of all let’s declare our data structure:
pub struct TriangularArray<T: Default + Clone> {
array: Vec<T>,
dimension: usize,
}Analysing the structure we can see that is composed of two fields, array that should contain the unique data only (essentially we store only the upper or lower triangular matrix) and dimension that reflects the size of the symmetrical matrix.
The data is stored in a (n × n + 1) ÷ 2 array, and this will save (n × n) - ((n × n + 1) ÷ 2) elements in memory.
To construct the structure we can use the following associate function:
pub fn with_dimension(size: usize) -> std::result::Result<TriangularArray<T>, String> {
if size > 0 {
let size = size * (size + 1) / 2;
Ok(TriangularArray {
array: vec![Default::default(); size],
dimension: size,
})
} else {
Err(format!(
"Invalid length size should be higher than 0 but is {}",
size
))
}
}First why do we need to return a Result? This is because the matrix needs to be at least of size 1. Next we calculate the size needed to store a matrix n × n and create a Vec of the calculated size with a default value for all the elements.
To get and set the value for a specific element we can use the following:
pub fn get_value(&self, rows_index: usize, columns_index: usize) -> Option<&T> {
self.array
.get(self.calculate_index(rows_index, columns_index))
}
pub fn get_value_mut(&mut self, rows_index: usize, columns_index: usize) -> Option<&mut T> {
let index = self.calculate_index(rows_index, columns_index);
self.array.get_mut(index)
}These methods are pretty simple, calculate the index and get/set the value from/into the array.
What is that method to calculate_index? Let’s discuss first how an index is calculated
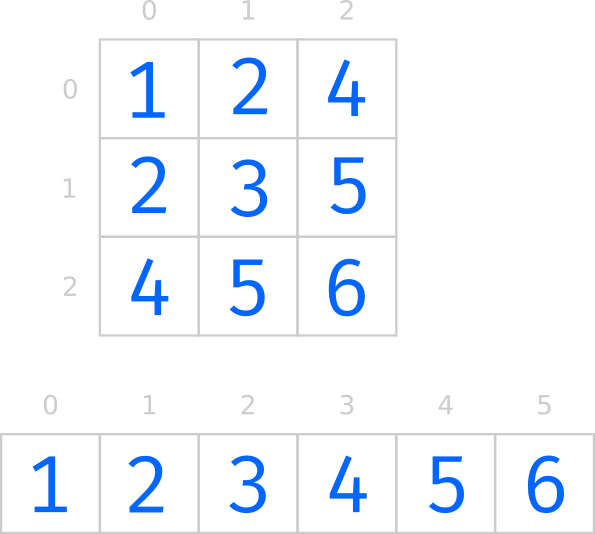
From the above matrix, we can see that to get the value 5 we can use the indices (1, 2) or the indices (2, 1). First of all what we need to understand is what kind of indices are passed and switch them to calculate the final value. Second we need to derive the formula to calculate the index, this is pretty simple: ((greater_index × ( greater_index + 1)) ÷ 2) + smaller_index this is because first we need to move to the correct row or column (depending on the indices order), next to the correct value using the smaller value.
The code should look like this:
fn calculate_index(&self, rows_index: usize, columns_index: usize) -> usize {
if cfg!(debug_assertions) {
self.check_boundaries(rows_index, columns_index);
}
if rows_index < columns_index {
columns_index * (columns_index - 1) / 2 + rows_index
} else if rows_index == 0 {
columns_index
} else {
rows_index * (rows_index - 1) / 2 + columns_index
}
}
fn check_boundaries(&self, rows_index: usize, columns_index: usize) {
assert!(
rows_index <= self.dimension,
"The row({}) must be smaller than the number of columns({})",
rows_index,
self.dimension,
);
assert!(
columns_index <= self.dimension,
"The column({}) must be smaller than the number of rows({})",
columns_index,
self.dimension,
);
}Note the followings on the calculate_index method:
- It checks first (only in debug but that should be enough) if the row and column indices are valid;
- it calculates the correct index based on the case;
- the special check against 0 is to not have an overflow using the usize.
This is how you can store a symmetric matrix in a more compact way using some indices math to keep the same behaviour.
See you next time!